Simplesso Duale

Si tratta di un metodo per risolvere il problema di PL primale nel caso in cui non sia valida l’ammissibilità primale (cioè ci sono termini noti negativi nella Forma Standard), ma sia verificata l’ammissibilità duale (cioè i costi ridotti delle variabili fuori base sono ).

Il metodo parte da una soluzione di base non ammissibile, cioè esterna al poliedro, e cerca di raggiungere la soluzione ottima.

Ad ogni iterazione i costi ridotti sono sempre e si cerca di avere tutti i termini noti

Per riassumere:

Simplesso Primale	Simplesso Duale
Condizioni: Termini Noti	Condizioni: C’è almeno un termine noto negativo; Costi ridotti
Obiettivo: Costi Ridotti	Obiettivo: Termini Noti

Criterio di Uscita

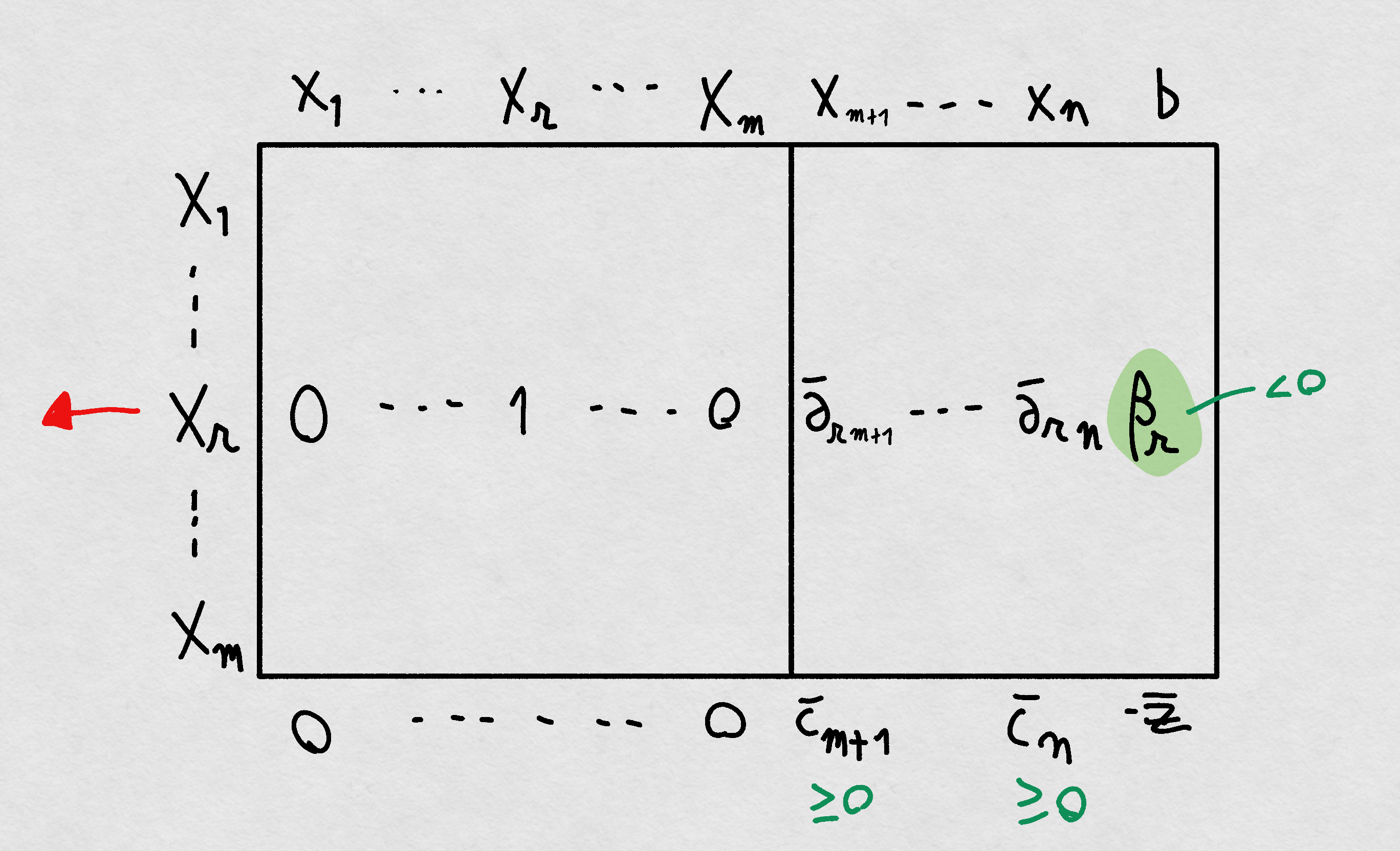
Esce dalla base la variabile associata al termine noto negativo

Si individua la riga , se gli elementi della riga sono TUTTI PROBLEMA PRIMALE INAMMISSIBILE 

Criterio di non ammissibilità

Se il primale è inammissibile il duale potrebbe essere non limitato o non ammissibile. 

Poichè vale la condizione di ammissibilità duale allora il problema duale non è limitato

Se ci sono elementi negativi sulla riga si individua la variabile uscente , dove è l’indice di colonna tale che

Criterio di Entrata

Resta individuato il pivot della trasformazione.

Riassumendo di nuovo:

Simplesso Primale	Simplesso Duale
Costo ridotto dà la variabile entrante	Termine noto dà la variabile uscente
Criterio Rapporto per la variabile uscente	Criterio rapporto per la variabile entrante
Criterio illimitatezza: Elementi colonna con costo ridotto negativo	Criterio di inammissibilità: Elementi riga associati ad un termine noto
Ottimalità: Costi ridotti	Ottimalità: Termini noti

Analisi di Post-Ottimalità

Supponiamo di causare la perturbazione di un termine noto

La soluzione di ottima di base è ,

Sia

(B^{-1}b,0) è ancora ottima?

Caso 1: ha componenti negative Non vale l’ammissibilità primale. 

I costi ridotti non hanno il vettore , quindi i costi ridotti sono ancora

(e sono perché è soluzione ottima).

Possiamo applicare il simplesso duale per calcolare la nuova soluzione ottima.

Caso 2: ha componenti è ammissibile