Convergenza del Metodo

Se nelle iterazioni del metodo si generano soluzioni di base non degenere (cioè con componenti di base ), allora la funzione obiettivo migliora ad ogni iterazione. Dopo un numero finito di iterazioni, il metodo si arresta. 

Se si incontrano delle soluzioni di base degeneri, allora può accadere di rimanere bloccati su un vertice. 

Risulta che data una base B si costruisce una soluzione di base .  

Una soluzione di base degenere (con componenti di base ) invece proviene da più basi.  

Se ci sono soluzioni di base degeneri non è garantito che sia senza ripetizioni. Cioè il metodo cicla, tornando su basi già visitate.

Riassumento

• Soluzioni di base non degenere proviene da una sola base (e ha componenti di base )
• Soluzioni di base degenere proviene da più basi (e ha componenti di base )

Regola di Bland

Si usa per evitare di ciclare. 

Se c’è indecisione sulla variabile entrante, (cioè ci sono più costi ridotti negativi), oppure sulla variabile uscente (cioè ci sono più rapporti minimi uguali), si sceglie sempre l’indice minimo.

Complessità

, nel caso medio è lineare in o in . Il numero delle iterazioni è circa .

Nel caso peggiore si ottiene un ipercubo di dimensione , in cui occorre visitare tutti i vertici per trovare l’ottimo.

Questo risulta in iterazioni necessarie per arrivare al vertice ottimo.

Unicità Soluzione

Se i costi ridotti delle variabili fuori base sono tutti strettamente positivi, allora la soluzione di base corrente è l’unica soluzione ottima.

Esempio 1

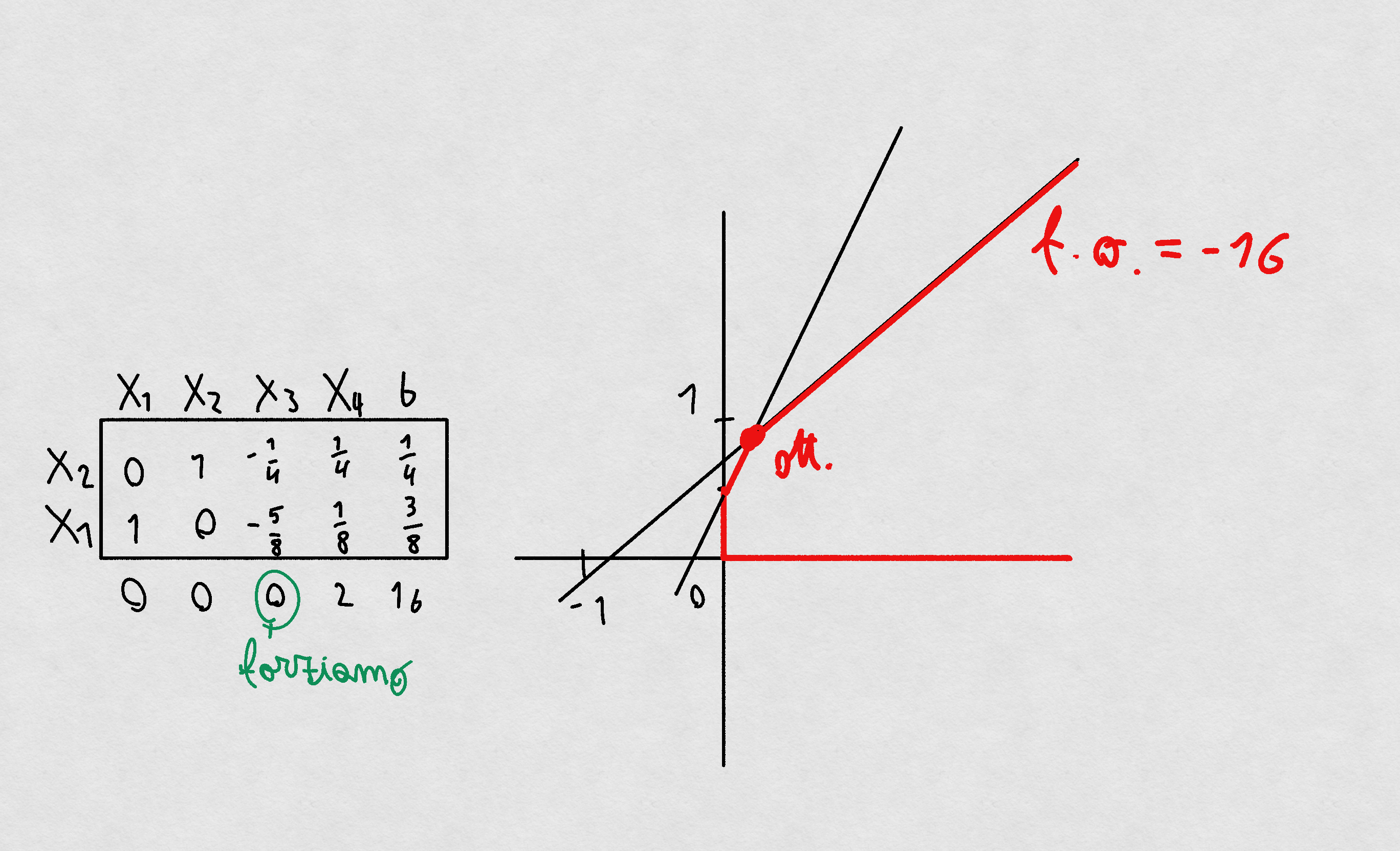
Vediamo direttamente la tabella finale.  

Si potrebbe pensare di ‘forzare’ il metodo facendo entrare in base , considerando il costo ridotto nullo. 

Ma gli elementi della colonna sono e quindi questo significa che il problema ha soluzioni ottime.

Generalmente risulta che sono ottimi […Scrittura incomprensibile… 😒] i punti della semiretta che ha origine nel vertice ottimo.

Esempio con Base Degenere

[Grafica WIP che non verrà mai fatta probably, lungo e poco utile da vedere]

Restiamo bloccati in un vertice.

In generale una soluzione di base degenere è una intersezione di vincoli dove è la dimensione del problema. Inoltre, di solito nei vertici vicini la f.o. avrà valore ‘meno ottimo’ rispetto al vertice di intersezione dove restiamo bloccati.