Rette nel piano
Una retta ha un’espressione del tipo
è un vettore ortogonale alla retta appena definita, che punta verso il semipiano Trasposto perché i vettori sono sempre in colonna.
I problemi di programmazione lineari in 2 variabili possono essere risolti graficamente.
Metodo Grafico
Si basa sulla rappresentazione geometrica della regione ammissibile, dei vincoli e della funzione obiettivo sul piano cartesiano.
Nei problemi di PL i vincoli sono disequazioni lineari
Ponendo i vincoli in forma di retta, otteniamo il grafico:
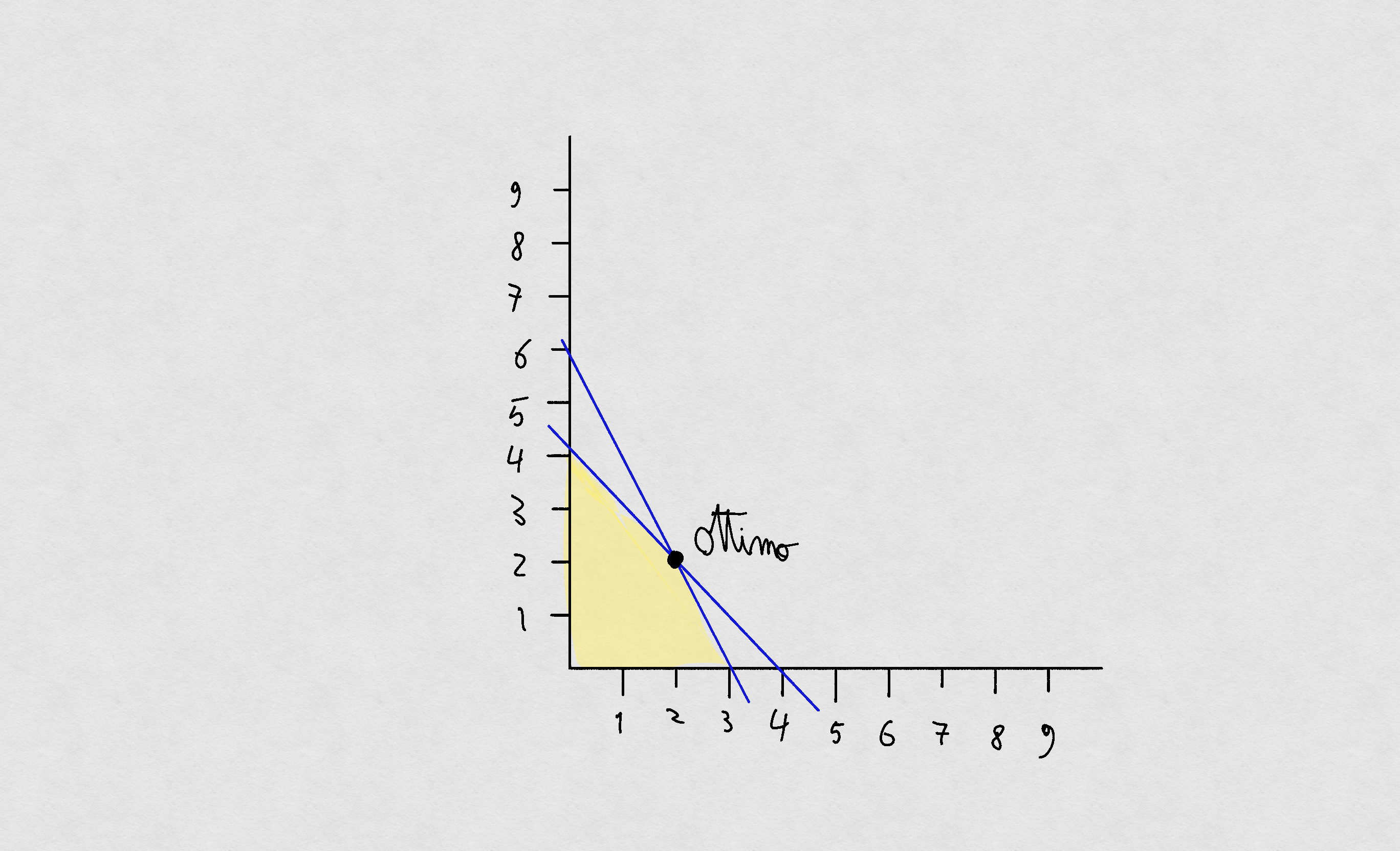
E difatti la soluzione ottima sarà il punto
Come scegliere il semipiano giusto
Si prende il punto test
e si sostituisce in , difatti in questo caso si ottiene , che è vero. Il semipiano giusto in questo caso è quello che contiene il punto test.
Osservazione
Se i coefficienti della funzione obiettivo non sono tutti nulli, la soluzione non è mai interna alla regione ammissibile. Quindi starà sul bordo.
Un’altra procedura è quella di considerare il fascio di rette generato dalle rette parallele e ortogonali a quella che rappresenta la funzione obiettivo, cioè quindi al vettore
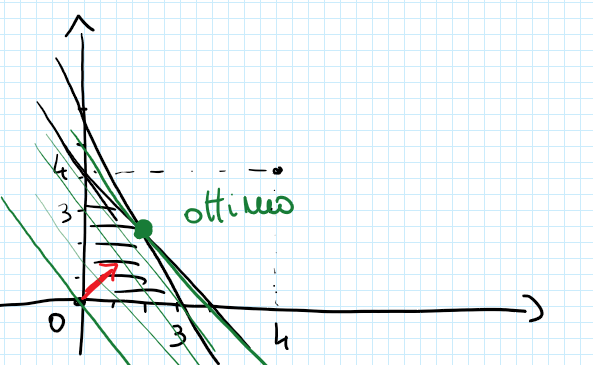
La soluzione ottima sarà l’ultimo punto ammissibile comune con la retta del fascio.
Procedura
- Rappresentiamo i semipiani di vincoli sul piano cartesiano;
- Per rappresentare la funzione obiettivo, tracciamo le linee di livello della f.o. , cioé il fascio di rette
al variare di k. - Le linee di livello sono parallele tra loro e ortogonali al vettore
. è il valore della f.o che dobbiamo max/minimizzare. - Per massimizzare: trasliamo la retta della f.o. seguento la direzione del vettore.
- Per minimizzare: andiamo in direzione opposta.
- Fra tutte le linee di livello prendiamo quella che ha il valore max (min) di k e si ottiene la soluzione prendendo l’ultimo punto comune tra la retta del fascio e la regione ammissibile