Problema dell'assegnamento

Siano A e B due insiemi tali che e .

Sono dati dei costi agli abbinamenti tra gli elementi di e .

Il problema degli assegnamenti consiste nell’assegnare ad ogni elemento di A un solo elemento di in modo che non ci siano elementi non accoppiati e il costo totale sia minimo.

Se si aggiungono elementi fittizi e costi nulli degli abbinamenti con elementi fittizi.

Formulazione Matematica

È un particolare problema del trasporto con domanda e offerta = 1.

La matrice dei coefficienti è Totalmente Unimodulare

Matrice Unimodulare

Matrice Unimodulare

Una matrice si dice totalmente unimodulare quando ogni sottomatrice di ordine ha determinante

Proposizione

Dato il poliedro con A matrice tot. unimodulare, e b intero poliedro ha solo vertici interi

Possiamo quindi risolvere il problema rilassato con il vincolo (insieme agli altri vincoli diventa poi solo) )

Non è utile usare il simplesso perché il poliedro ha vertici fortemente degeneri, si usa infatti un algoritmo specifico:

Algoritmo Ungherese

Opera sulla matrice dei costi e trasforma la matrice dei costi in una serie di matrici equivalenti fino a determinare l’assegnamento di costo minimo che corrisponderà al ricoprimento degli zeri della matrice.

Operazioni

1. Si sottrae ad ogni riga il suo elemento minimo: (generiamo zeri sulle righe)
2. Si sottrae ad ogni colonna il suo elemento minimo: (generiamo zeri su colonne)
3. Si cerca l’assegnamento di costo minimo, cercando il ricoprimento degli zeri della matrice. Se il numero di righe e colonne che ricoprono gli zeri è minore del numero di righe della matrice, l’assegnamento non è completo e si deve ridurre ancora la matrice. Altrimenti, si è trovato l’assegnamento completo di costo minimo
4. Si barrano le righe e le colonne che ricoprono gli zeri. Sia l’elemento minimo non barrato. Si aggiunge agli elementi barrati 2 volte (cioè l’incrocio tra riga e colonna) e si sottrae agli elementi non barrati.

Si ripetono e fino a trovare l’assegnamento completo

Regola generale per trovare il ricoprimento minimo degli zeri

• Si etichettano le righe lasciate fuori dall’assegnamento;
• Si etichettano le colonne che hanno degli zeri in corrispondenza delle righe etichettate;
• Si etichettano le righe abbinate alle colonne etichettate dall’assegnamento ottenuto;
• Si barrano le righe non etichettate e le colonne etichettate.

Link to original

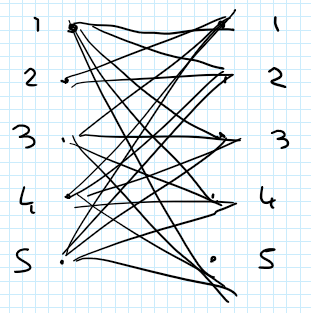
Assegnamento su Grafo Bipartito

Il problema dell’assegnamento si può vedere su un grafo bipartito completo. Siano noti i costi su tutti gl iarchi e si cerca un abbinamento tra gli elementi dei due insiemi di costo minimo.