📚 Algoritmi

Search

SearchSearch

Minimum Spanning Tree

Mar 06, 2024, 6 min read

Alberi Ricoprenti Minimi

Input:

  • Grafo non Orientato Connesso:
  • Una funzione peso Output:
  • Albero con , tale che per ogni altro albero , con si abbia:
    • Cioè un albero la cui somma di tutti i pesi dei suoi archi è minore o uguale a quella di ogni altro albero possibile.  

Algoritmo semplice: ricerca esaustiva di un MST. 

Problema: la ricerca esaustiva è però esponenziale, infatti il numero di alberi ricoprenti in un grafo completo su vertici è . 

Discutiamo tre algoritmi Greedy:

Sono tutti basati su un processo, non deterministico, di colorazione che mantiene un opportuno invariante (invariante del colore). 

A seconda dell’euristica utilizzata nel processo di colorazione si otterranno i tre algoritmi sopra. 

In generale, si scelgono gli archi , e si eliminano gli archi .

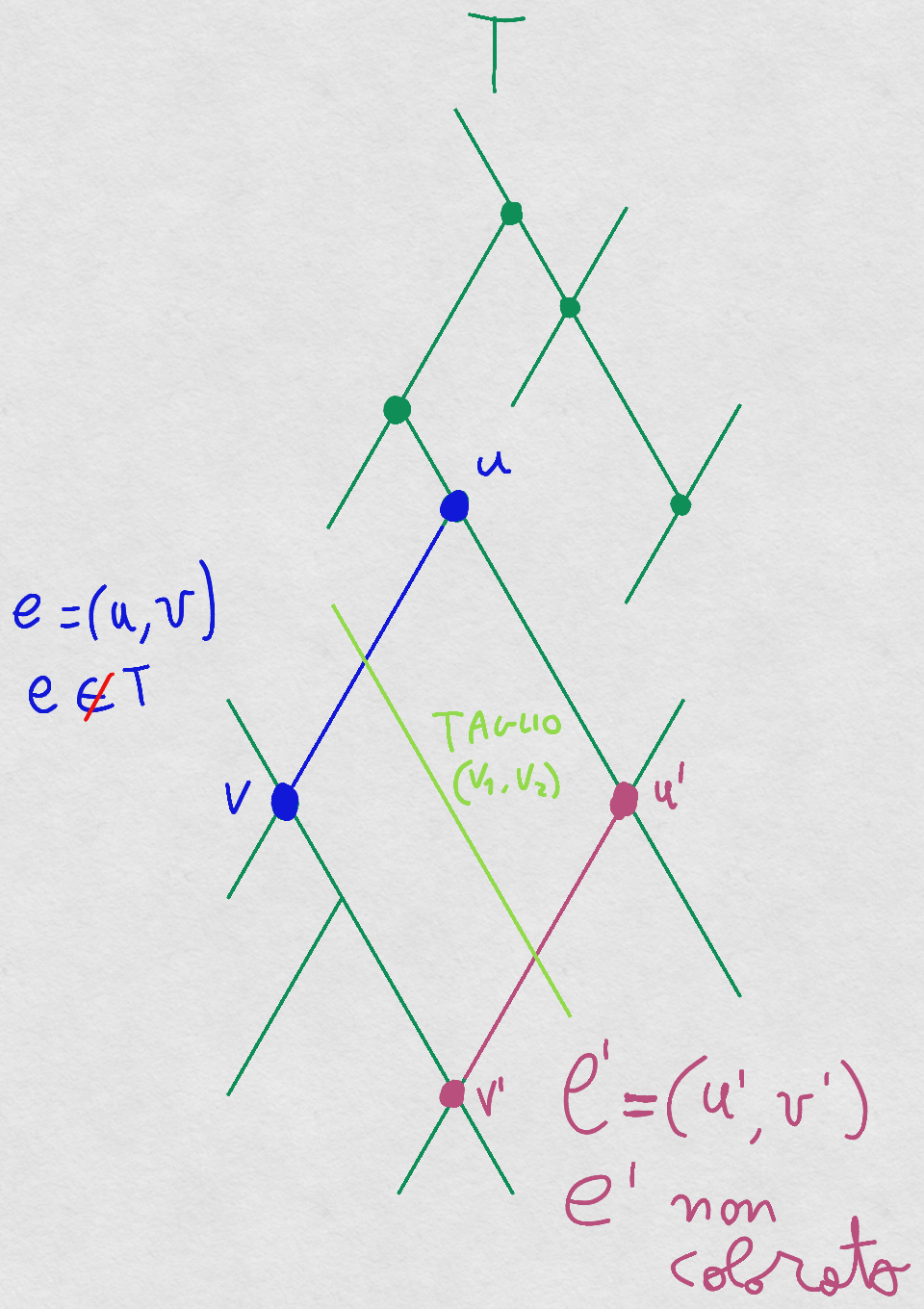
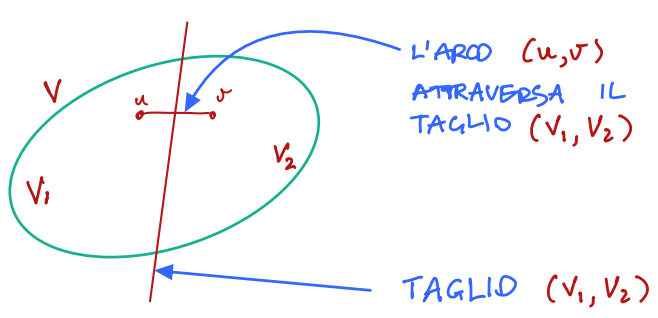
Taglio

Definizione

Un Taglio di è una partizione di non banale (cioè tale che ). 

Un arco tale che e si dice che attraversa il taglio .

Processo di Colorazione

Inizialmente nessun arco è colorato.

Finchè è possibile, si applichi uno dei due passi: 

    • Si seleziona un taglio non attraversato da alcun arco blu;
    • Tra gli archi non colorati che attraversano il taglio se ne selezioni uno di peso minimo e lo si colori di .
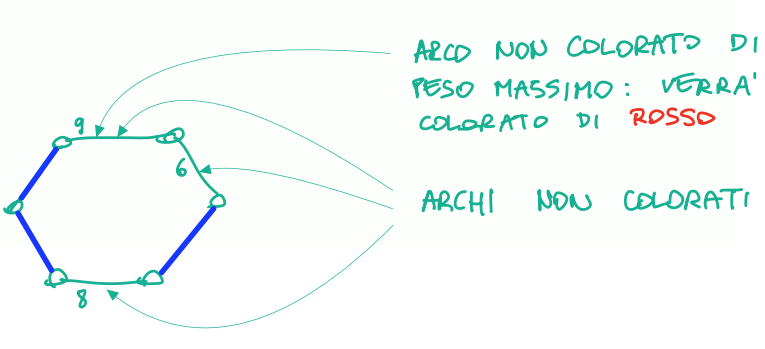
    • Si seleziona un ciclo semplice privo di archi rossi;
    • Tra gli archi non colorati del ciclo se ne selezioni uno di peso massimo e lo si colori di .  

In un ciclo semplice: 

I tre algoritmi sono tutti istante di questo processo di colorazione. Dimostrando che la colorazione è corretta, tutte le sue istanze, di conseguenza, lo saranno.

Durante l’esecuzione del processo di colorazione vale la:

Invariante del Colore

Definizione

Ad ogni passo della procedura di colorazione esiste un MST contenente tutti gli archi e nessun arco .

Teorema

Ogni esecuzione del processo di colorazione colora tutti gli archi mantenendo l’invariante del colore.

Corollario con DIM

Alla fine della procedura di colorazione, l’insieme degli archi forma un MST 

Dimostrazione

  • Sia l’insieme degli archi blu alla fine del processo,
  • Sia un MST tale che (che esiste grazie all’invariante del colore),
  • Poiché non contiene alcun arco rosso, si ha anche il viceversa, cioè
  • Quindi è un MST

Verifichiamo che l’invariante d el colore è mantenuto dopo ogni passo di colorazione, per induzione. 

  • Inizialmente l’invariante del colore è banalmente verificato, in quanto non ci sono nè archi blu, nè archi rossi.
  • Ipotesi Induttiva: Sia un MST che contiene tutti gli archi blu al passo , e nessun arco rosso  

Passo k+1  

Caso: il passo colora di l’arco che attraversa il taglio privo di archi blu. 

  • Se verifica l’invariante del colore anche al passo .
  • Se , si consideri il cammino in da a .
    • Sia un arco su tale cammino che attraversa il taglio . Esso è non colorato.
  • Si consideri ora tale che:
  • Poichè si ha  

Cioè è un MST contenente tutti gli archi blu al passo . 

In altre parole: 

L’arco , appena colorato di blu al passo , nasce da un taglio. Supponiamo di essere nel caso in cui non appartiene all’MST . 

Considerando un arco sul cammino in da a . Questo arco:

  • Attraversa il taglio;
  • Non può essere rosso perché non avevamo archi rossi al passo precedente;
  • Non può essere blu perché abbiamo appena colorato di blu l’arco . Quindi è non colorato. 

A questo punto vale la relazione perché T è un MST. 

Ma dato che T è un MST,vllora vale anche . 

Questo ci fa concludere che e sono uguali, quindi anche è un MST.

Due domande che potremmo porci a questo punto sono:

  • “ma è ancora un albero?” Sì, perché la cardinalità degli archi è uguale
  • ”Ma dopo che esce l’albero è ancora connesso?” Sì, perché un albero è un grafo connesso minimale.

Passo k+1  

Caso: il passo k+1 colora di l’arco relativo al ciclo semplice  

  • Se non c’è niente da dimostrare.
  • Supponiamo allora che , perché potrebbe non mantenere l’invariante.
  • ha due componenti connesse che determinano una partizione di .
  • Sia un arco sul cammino che attraversa il taglio .
    • Si noti che non può essere blu perché .
    • Inoltre non può essere rosso perché il ciclo semplice scelto per effettuare il passo non contiene archi rossi
    • Pertanto non è colorato.

Sia tale che . è uno spanning tree. 

 

Quindi è un MST che verifica l’invariante del colore. 

L’albero è ancora connesso? sì, le 2 componenti connesse da sono ora connesse da

Lemma

Al termine dell’esecuzione della colorazione, tutti gli archi sono stati colorati.

Dimostrazione 

  • Sia un arco non ancora colorato,
  • Sia un MST che verifica l’invariante del colore,
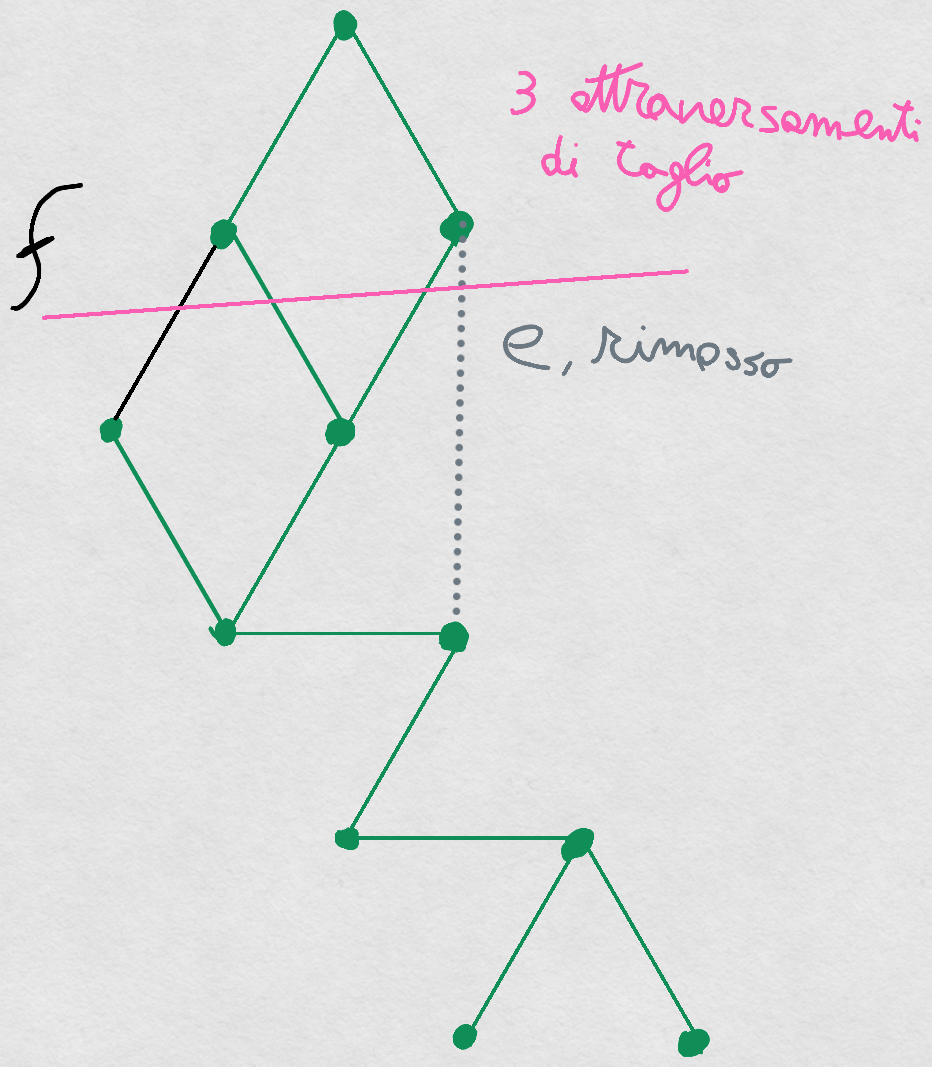
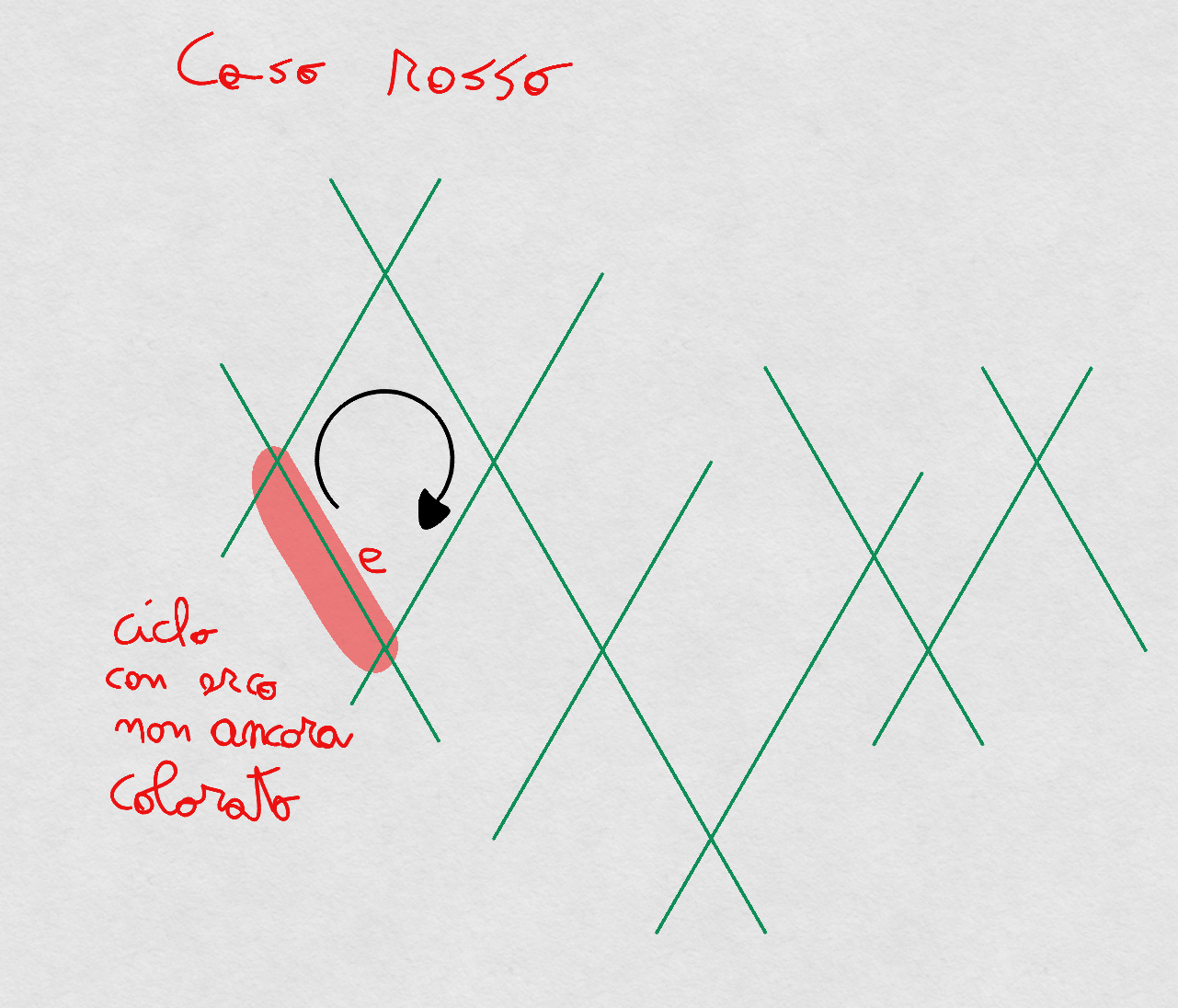
  • Se , cancellando da si ottengono due componenti connesse che determinano un taglio
  • non è attraversato da alcun arco ed è attraversato da archi non colorati è possibile applicare un passo
  • Se , sia il cammino da a in , e si consideri il ciclo semplice
  • Tale ciclo non contiene archi ed inoltre contiene archi non colorati è possibile applicare un passo a tale ciclo.

Unicità MST

Proprietà

Sia un grafo non orientato e connesso con funzione peso iniettiva ha un unico MST.

Reminder:

Dimostrazione

Siano due MST di . 

Sia di peso minimo. 

Supponiamo che , sia un cammino da a in , ovviamente  

Sia . 

Pertanto . 

Sia ora , si ha che è un albero. 

Inoltre , cioè che è un altro MST con peso minore a , che è assurdo.

Spiegazione più grafica e discorsiva di questa cosa apparentemente brutta brutta:

MST: Argomenti affini

Separati per mantenere ordine

Graph View

Backlinks