Union-Find

Strutture dati per insiemi disgiunti

• è spesso utile rappresentare in maniera efficiente famiglie dinamiche di insiemi disgiunti soggette alle seguenti operazioni:
  • Make_Set(x): Introduzione del singoletto
  • Union(x,y): Unioni degli insiemi disgiunti che contengono rispettivamente x e y
  • Find_Set(x): Ricerca dell’insieme che contiene x
• Tali operazioni consentono la gestione di relazioni di equivalenza dinamiche monotone non-decrescenti.
• Analizzeremo seguenze di operazioni Make_Set, Union e Find_Set comprendenti n operazioni Make_Set, a partire da una configurazione vuota.
• Ovviamente:
  •   Esempio di una semplice applicazione: Mantenimento delle componenti connesse in un grafo non orientato crescente.

Implementazione di insiemi disgiunti

Una possibile implementazione è con Liste Concatenate. 

Serve un puntatore da ciascun elemento al primo elemento della lista. 

è utile mantenere un puntatore all’ultimo elemento di ciascuna lista (tail), e conviene concatenare la seconda lista alla prima, durante l’esecuzione di una Union. 

Per eliminare il campo tail: la ricerca della coda della seconda lista si può fare mentre si aggiornano i campi della seconda lista.

Nell’eseguire l’operazione di Union, si appena la lista più corta a quella più lunga. (Unione per Ranghi) 

Complessità

• Data una sequenza di operazioni Make_Set, Union, e Find_Set, poniamo:
• La complessità della sequenza è chiaramente:

I costi ammortizzati delle operazioni sono:

• Find_Set(x) = Union(x,y) =
• Make_Set(x) =

Calcoliamo in funzione di

• Quante volte può cambiare il valore in un nodo ?
• Per l’euristica dell’Unione per Ranghi, ogni qualvolta il valore è aggiornato, la lunghezza della lista che contiene aumenta almeno volte.
• Quindi, il campo può cambiare al più volte.
• Di conseguenza, il numero totale di aggiornamenti al campo di tutti i nodi è
• Pertanto la complessità della sequenza è

Rappresentazione di insiemi disgiunti con alberi disgiunti

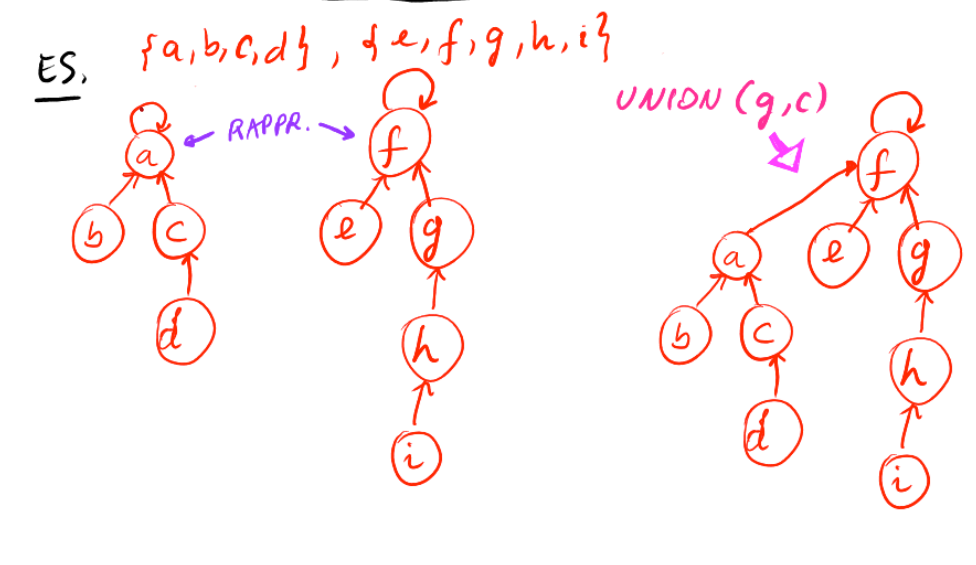
Euristiche:

Efficienza

L’implementazione con alberi disgiunti non è più efficiente di quella con liste concatenate, a meno che non si utilizzino le euristiche.

Per quanto concerne l'esame, ci interessano principalmente le due euristiche fondamentali di implementazione, ossia:

• Unione per Ranghi
• Compressione dei Cammini

Unione per Ranghi

• Si definisce opportunamente la nozione di Rango di un albero (legata in qualche modo all’altezza).
• Quindi si sceglie di innestare l’albero di rango più piccolo nella radice dell’albero di rango più alto.
• Nel caso di alberi aventi lo stesso rango, gli alberi si innestano in maniera arbitraria e il rango dell’albero risultante sarà incrementato di un’unità.

Compressione dei Cammini

• Tutti i nodi incontrati nell’esecuzione di una vengono innestati nella radice.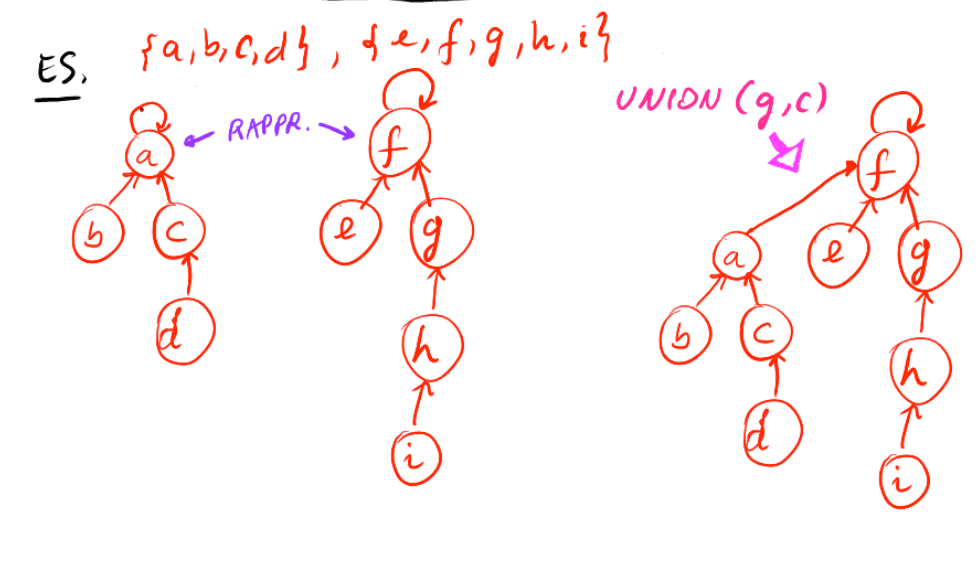

Effetto delle Euristiche sulla complessità

• La sola Unione per ranghi (senza compressione cammini) dà luogo a complessità .
• La sola Compressione dei Cammini (senza unione ranghi) dà luogo a complessità dove f=.
• Utilizzando entrambe le euristiche, si ottiene una complessità dove è la Funzione di Ackermann.
  • In pratica, sebbene

Pseudo-Codice delle operazioni:

Make_Set(x):
p[x] = x
rank[x] = 0

 

Find_Set(x):
if (x != p[x])
	p[x] = FIND_SET(p[x])
return p[x]

 

Link(x,y):
if (rank[x]>rank[y])
	p[y] = x
else
	p[x] = y
		if (rank[x] == rank[y])
			rank[y]++

 

Union(x,y):
Link(FIND_SET(x),FIND_SET(y))