Heap di Fibonacci

Uno Heap di Fibonacci è una collezione di alberi con la proprietà Heap.    Gli alberi di uno Heap di Fibonacci non devono necessariamente essere binomiali. 

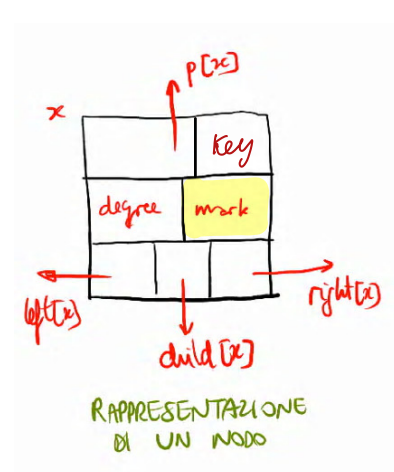
• : Padre;
• Fratello sinistro;
• Fratello destro;
• un figlio;
• numero di figli;
• indica se il nodo ha perduto un figlio dall’ultima volta in cui è diventato figlio di un altro nodo.

Inoltre:

• punta al minimo, indica la radice contenente la chiave minima e dà accesso alla struttura;
• contiene il numero di nodi in H.

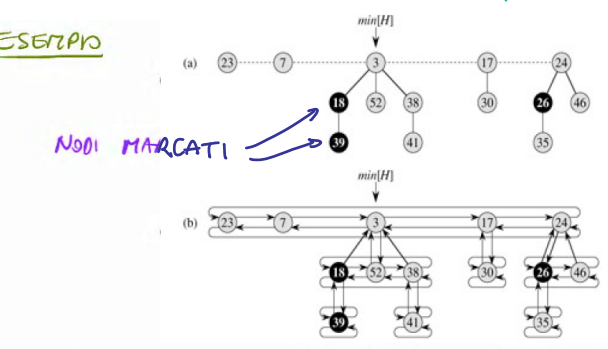
Esempio

Funzione Potenziale

Dove:

• t(H): numero alberi nella lista delle radici di H;
• m(H): numero nodi marcati in H
• Sia una collezione finita di Heap, poniamo:  

Stima di D(n)

è il massimo grado di un nodo. 

• L’analisi verrà effettuata in funzione di un upper bound sul massimo grado di un nodo qualunque in uno heap con n nodi.
• Dimostreremo che si ha:

Operazioni presenti e mancanti

Se vengono eseguite SOLO operazioni del tipo:

• Make-Heap;
• Insert;
• Minimum;
• Extract-Min;
• Union.

Ciascuno Heap di Fibonacci è rappresentabile come collezione di alberi binomiali non ordinati. 

massimo grado di un nodo in un heap di fibonacci con nodi costruito senza mai usare le operazioni di Decrease-Key e Delete.

Vedremo che . Inoltre, i costi di complessità sono ammortizzati.

Lemma 3 (quello che c’è all’esame da qui in poi, ndr)

(Abbiamo saltato i primi due perché indicano proprietà dei numeri di fibonacci). 

Sia un nodo in un heap di fibonacci e sia . 

Siano i figli di nell’ordine in cui sono stati innestati in . 

Allora, per

Dimostrazione

Sia ; notiamo che quando è innestato in , al tempo T, il nodo ha già . 

Tra i suoi figli, per cui . 

Dall’istante T, può avere perduto al più un figlio, e quindi:

Altro Lemma

Sia x un nodo in uno heap di fibonacci, e sia . 

Allora dove è il numero di nodi nel sottoalbero radicato in .

Dimostrazione

…

Corollario 1

Corollario 2

da cui .

Dimostrazione