Algoritmo di Kruskal

Strategia

Seguendo un ordine non decrescente per costi, se l’arco corrente è contenuto in un albero lo si colori di , altrimenti lo si colori di .

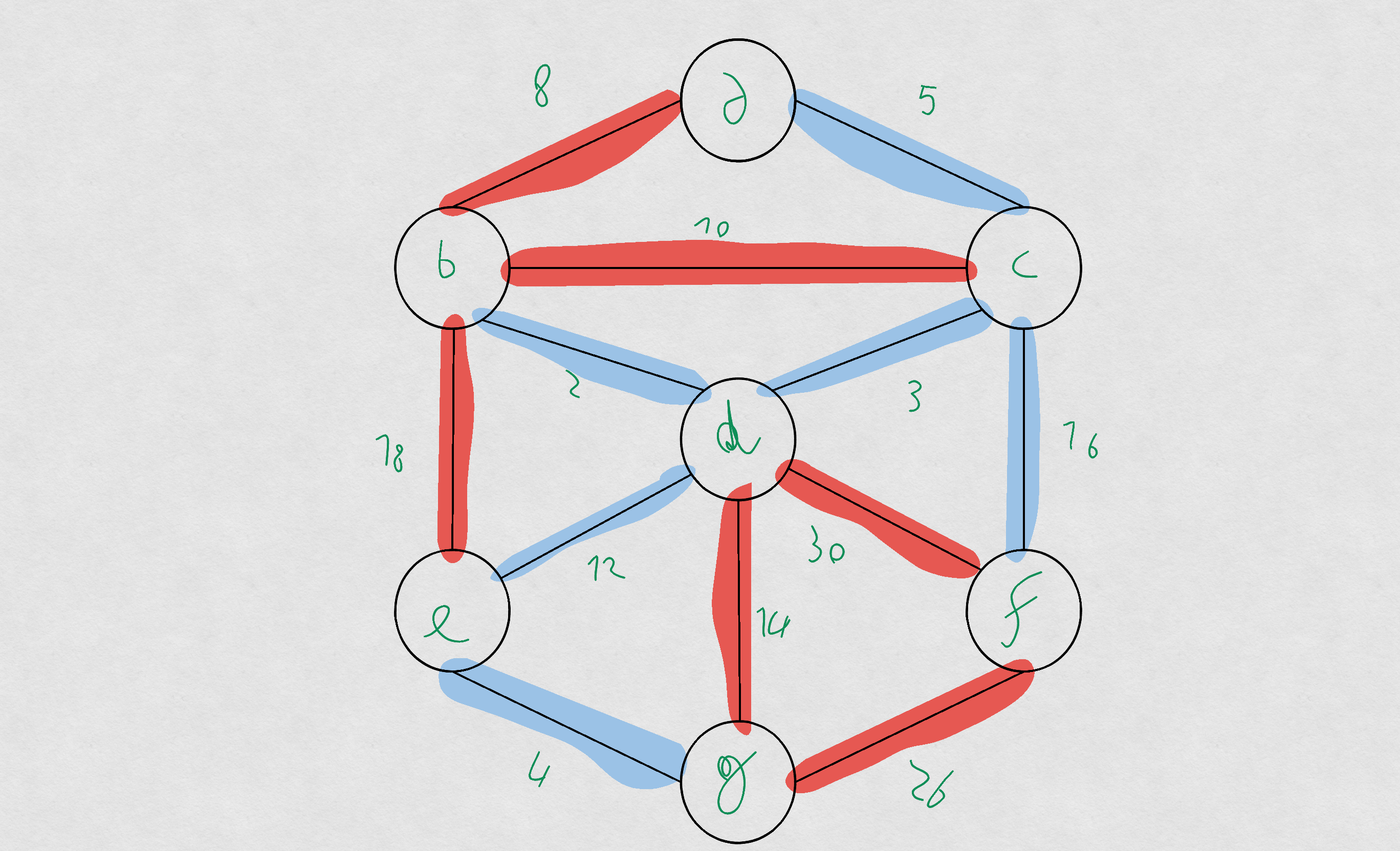
Esempio

Ordinamento

Colorazione

Oppure, per una strategia senza colori: ordina gli edge in ordine non-decrescente, come da pseudocodice (vedi sotto), crea un set per ogni vertice del grafo, e controlla via via in ordine di peso se due vertici sono nello stesso subset. 

Se sono in subset diversi, aggiungi l’arco nell’MST, e unisci il subset precedentemente disgiunto. 

Seguendo questo ragionamento senza sbagliare, avremo un MST corretto senza cicli.  

La riga 6 dello pseudocodice (l’istruzione if ) garantisce che il vertice e il vertice sono in subset diversi, garantendo appunto l’assenza di cicli.

Correttezza

• Sia l’ordinamento per pesi utilizzato;
• Siano le operazione di colorazione effettuate dall’algoritmo di Kruskal.
• Procediamo per induzione su  

Caso: colora di : 

• Sia
• Si ha che e appartengono a due alberi blu distinti
• Si consideri il taglio
• Esso è attraversato dall’arco
• Si osservi che tutti gli archi tali che sono già colorati.
• Pertanto ha peso minimo tra tutti gli archi non colorati che attraversano il taglio
• Pertanto può essere colorato da un passo

Caso: colora di : 

• Sia
• e appartengono ad uno stesso albero blu
• Sia il cammino da a in
• Si consideri il ciclo
• Tale ciclo non contiene archi rossi ed inoltre è l’unico arco non colorato
• Pertanto può essere colorato da un passo

Implementazione

Pseudocodice:

Kruskal(G,w)

T = EMPTY_SET();                             // T is going to be the MST
foreach (v in V)
	MAKE_SET(v)                              // create a subtree for each vertex
E = sort(E,w);                               // non-decreasing order
foreach ((u,v) in E)                         // in sorted edges...
	if (FIND_SET(u) != FIND_SET(v))          // if u and v are in different subtrees (sets), avoid cycles
		T = T U {(u,v)}                  // insert the edge inside the MST
		UNION(u,v)                       // union between the two different subtrees (sets), we're sure there are no cycles.
return T;                                    // return the MST

Complessità

 

Infatti si ha:

• : ordinamento degli archi
• Union-Find:
  • MAKE_SET
  • FIND_SET
  • UNION
  • operazioni, di cui MAKE_SET