MST-Segnatura

Distanza tra due Spanning Tree

Distanza

Siano e spanning tree di un medesimo grafo connesso .

Definiamo la distanza tra e ponendo:  

Segnatura Grafo Pesato

Sia un grafo non orientato con un funzione peso .

Segnatura

La Segnatura è la sequenza dei pesi degli archi di in ordine non decrescente.

Unicità della Segnatura

Teorema

Due qualunque MST di uno stesso grafo pesato non orientato e connesso hanno la medesima segnatura.

Dimostrazione

• Procediamo per assurdo:

• Sia un grafo non orientato connesso e pesato, con e , contenente degli MST con segnature distinte

• In particolare, siano e due MST di con segnature distinte, e tali che la loro distanza sia minima.

• Sia un arco di peso minimo in senza perdita di generalità, possiamo supporre che appartenga a , e non a .

• Sia il taglio di indotto cancellando l’arco dall’MST

• Sia un cammino in da a , e sia un arco in che attraversa il taglio

• Per la minimalità di in , si ha

• Pertanto, posto si ha che:

  • è uno spanning tree di ,
  • e
  • da cui e quindi e è un MST di G

• Si noti inoltre che:

  • Questo perché
  • e quindi:
  • contraddicendo la minimalità di

• Questa contraddizione deriva dall’aver supposto che possano esistere grafi pesati non orientati e connessi dotati di MST con segnature distinte. Pertanto il teorema risulta dimostrato

• Cammino

• 

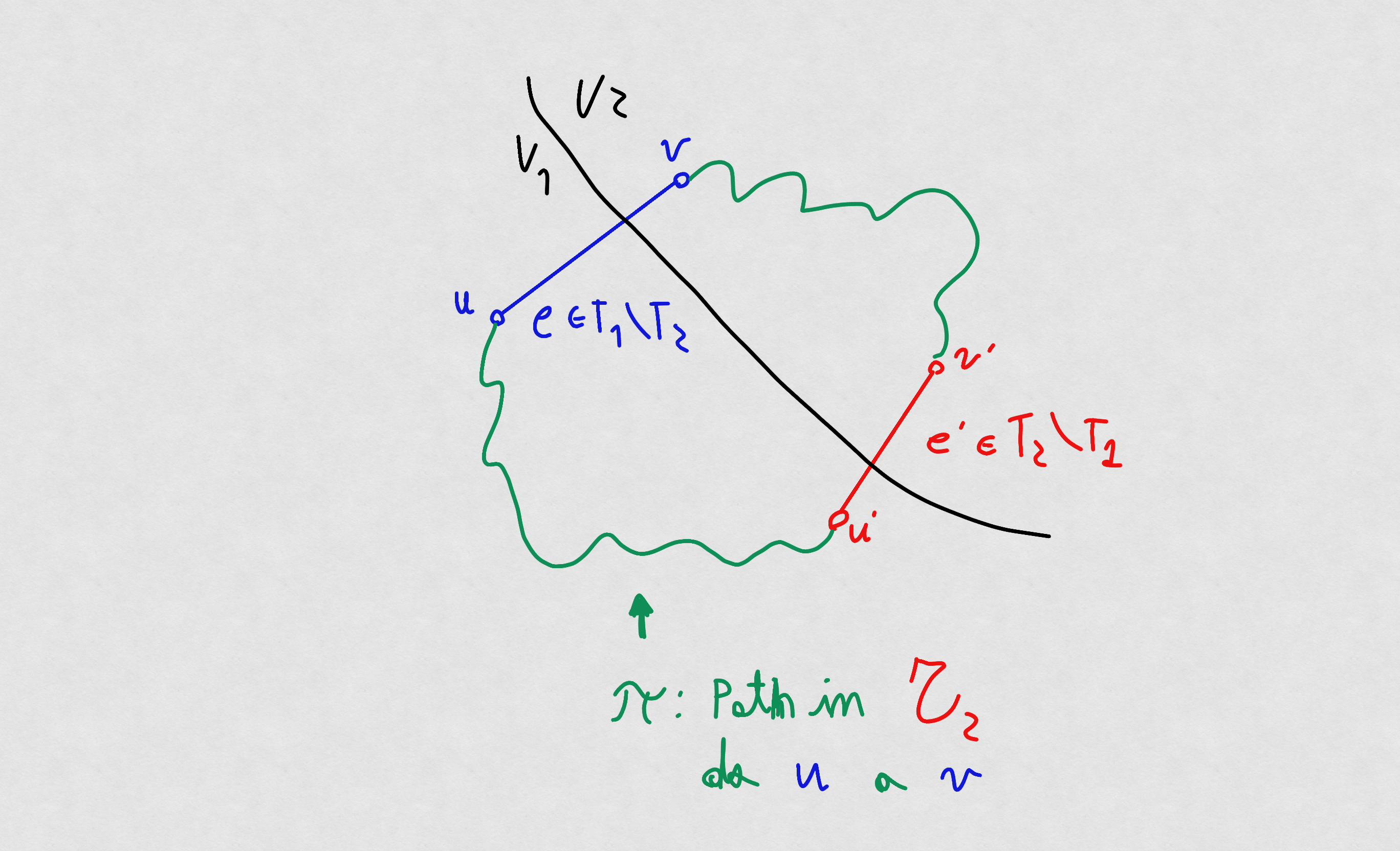
• Visualizzazione distanze con rimosso:

• 

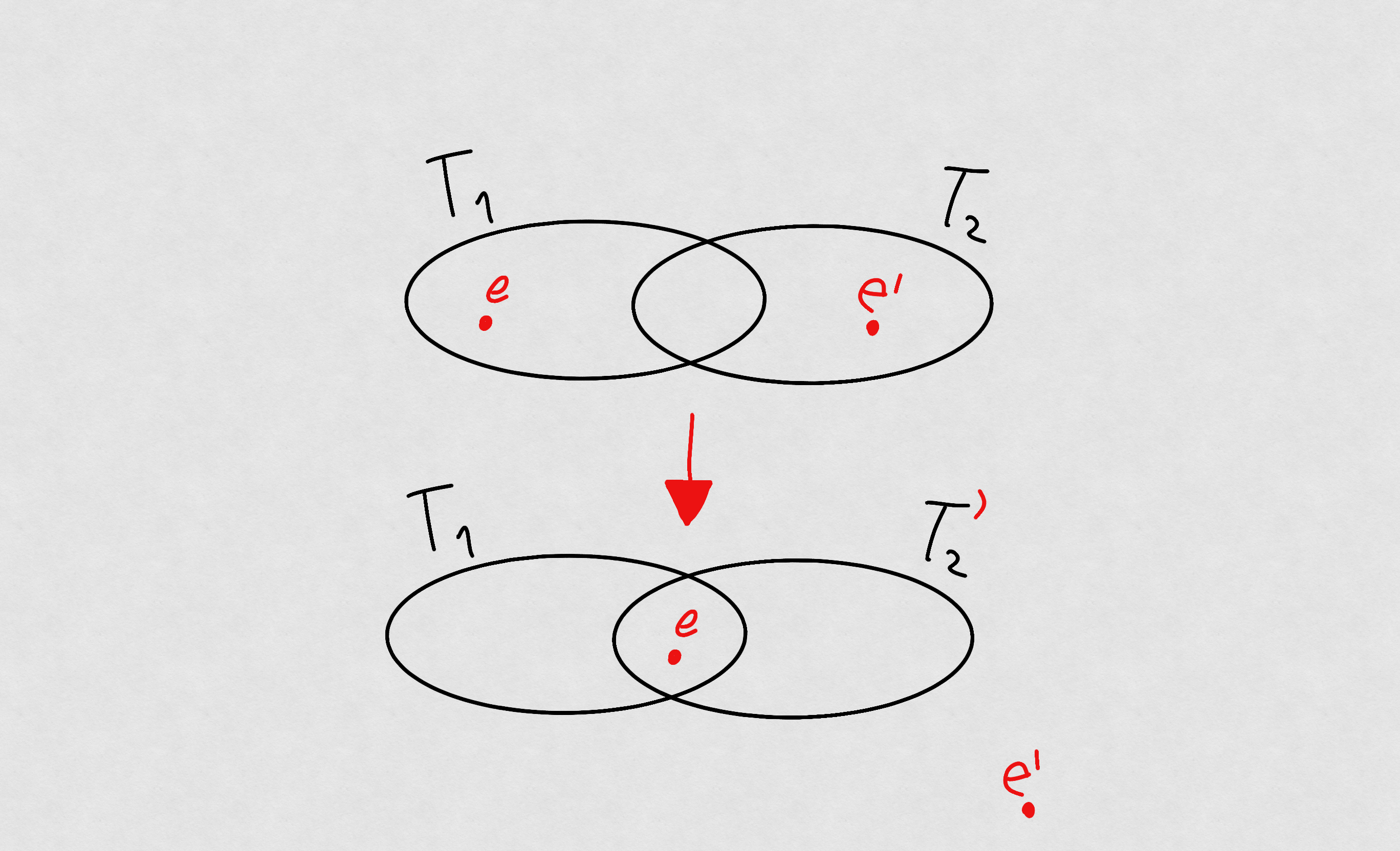
Corollario

Un grafo non orientato e connesso con funzione peso iniettiva ha unico MST

Dimostrazione

Sia la segnatura degli MST di un grafo con funzione peso iniettiva. 

Dall’iniettività di segue immediatamente che G ha un unico MST, cioè quello di segnatura

facile eh?

Minimalità della Segnatura

• Siano due di numeri reali, con lessicograficamente.
• Cioè se e solo se: per qualche .
• Esempio: precede

Proprietà A

La relazione di precedenza lessicografica tra è transitiva.

Proprietà B

Sia un grafo non orientato pesato, con e sia una qualunque funzione peso tale che:

• per qualche

Allora la segnatura di precede la segnatura di .

Teorema Minimalità

Teorema

Uno spanning tree è un MST se e solo se la sua segnatura è lessicograficamente minima

Dimostrazione

Procediamo per assurdo, supponendo che esista un grafo pesato non orientato e connesso, con , i cui MST hanno una segnatura non minima. 

Siano , con una coppia di spanning tree tali che:

Inoltre: sia di peso minimo, con . 

Abbiamo due casi:

• Caso

  • Sia il taglio di G indotto cancellando l’arco dall’MST . 
  • Sia un cammino in da a e sia un arco in che attraversa il taglio
  • Pertanto
  • Poiché è uno spanning tree, si ha:
  • Ma in tal caso avremmo , che contraddice la minimalità di

• Caso

  • Sia il taglio di G indotto cancellando l’arco dall’MST . 
  • Sia un cammino in da a e sia un arco in che attraversa il taglio
  • Caso analogo al prima, è uno spanning tree di G.
  • Poiché , si ha che:
  • Si ha dunque
  • Inoltre, per la stessa relazione sulla distanza, la coppia contraddice la minimalità di

Dimostrazione

Sia uno spanning tree di con segnatura minima, e sia un MST di G. 

Per la prima parte del teorema, la segnatura di è minima, dunque , pertanto anche è un MST.