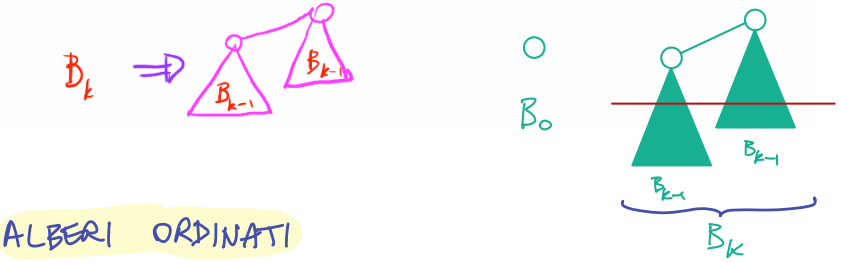Alberi Binomiali

Definizione

, definito in base alla seguente ricorsione:

• è l’albero formato da un solo nodo;
• Dato definiamo combinando due copie di nella seguente maniera:

Lemma (Proprietà degli alberi binomiali)

Per ogni valgono le seguenti proprietà: 

1. ha nodi;
2. L’altezza di è ;
3. ha nodi a profondità
4. La radice di ha grado ed ogni altro nodo in ha grado . Inoltre, i figli della radice di sono radici di nell’ordine dato. 

DImostrazione per induzione 

Caso Base:  

1. ha nodi.
2. L’altezza di è
3. ha nodi a profondità
4. La radice di ha grado

Passo Induttivo: Supponiamo che il Lemma sia vero per , con

1. ha nodi.

2. L’altezza di è

3. Sia , il numero di nodi di a profondità è uguale a:  

   Inoltre, ha nodi a profondità 0, quindi avrà nodi a profondità .

4. La radice di ha grado

   • Inoltre ciascun altro nodo appartiene ad un e pertanto per ipotesi induttiva ha grado , cioè .
   • Il primo figlio della radice di è radice di . Inoltre, per ipotesi induttiva, I successivi figli della radice di sono radici di

Corollario

Sia un albero binomiale con nodi, allora ogni nodo in ha al più grado . 

DImostrazione 

Per qualche si ha . 

Quindi .  

Ogni nodo in ha grado . 

Ma , da cui la tesi

 

Una foresta di alberi binomiali implementa un Heap Binomiale H.